LBNF reference¶
Introduction¶
This document defines the grammar formalism Labelled BNF (LBNF), which is used in the compiler construction tool BNF Converter. Given a grammar written in LBNF, the BNF Converter produces a partial compiler front end consisting of a lexer, a parser, and an abstract syntax definition. Moreover, it produces a pretty-printer and a language specification in LaTeX, as well as a template file for the compiler back end. Since LBNF is purely declarative, these files can be generated in any programming language that supports appropriate compiler front-end tools. As of Version 2.8.3, code can be generated in Agda, C, C++, Haskell, Java, and Ocaml. This document describes the LBNF formalism independently of code generation, and is aimed to serve as a manual for grammar writers.
A first example of LBNF grammar¶
As the first example of LBNF, consider the following grammar for expressions limited to addition of ones:
EPlus. Expr ::= Expr "+" Number ;
ENum. Expr ::= Number ;
NOne. Number ::= "1" ;
Apart from the labels EPlus, ENum, and NOne, the rules are ordinary
BNF rules, with terminal symbols enclosed in double quotes and
nonterminals written without quotes. The labels serve as constructors
for syntax trees.
From an LBNF grammar, the BNF Converter extracts an abstract syntax and a concrete syntax. In Haskell, for instance, the abstract syntax is implemented as a system of datatype definitions:
data Expr = EPlus Expr Number | ENum Number
data Number = NOne
For other languages, like C, C++, and Java, an equivalent representation is given, following the methodology defined in Appel’s book series Modern compiler implementation in ML/Java/C [1]. The concrete syntax is implemented by the lexer, parser and pretty-printer algorithms, which are defined in other generated program modules.
LBNF in a nutshell¶
Basic LBNF¶
Briefly, an LBNF grammar is a BNF grammar where every rule is given a label. The label is used for constructing abstract syntax trees whose subtrees are given by the nonterminals of the rule, in the same order.
More formally, an LBNF grammar consists of a collection of rules, which have the following form (expressed by a regular expression; the Appendix: LBNF Specification gives a complete BNF definition of the notation):
Identifier "." Identifier "::=" (Identifier | String)* ";"
The first identifier is the rule
label, followed by the value category. On the right-hand side of the
production arrow (::=) is the list of production items. An item is
either a quoted string (terminal) or a category symbol
(non-terminal). A rule whose value category is 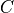 is also
called a production for
is also
called a production for 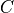 .
.
Identifiers, that is, rule names and category symbols, can be chosen ad libitum, with the restrictions imposed by the target language. To satisfy C, Haskell and Java, the following rule is imposed:
An identifier is a nonempty sequence of letters, digits, and underscores, starting with a capital letter, not ending with an underscore.
Additional features¶
Basic LBNF as defined above is clearly sufficient for defining any context-free language. However, it is not always convenient to define a programming language purely with BNF rules. Therefore, some additional features are added to LBNF: abstract syntax conventions, lexer rules, pragmas, and macros. These features are treated in the subsequent sections.
Section Abstract syntax conventions explains abstract syntax conventions. Creating an abstract syntax by adding a node type for every BNF rule may sometimes become too detailed, or cluttered with extra structures. To remedy this, we have identified the most common problem cases, and added to LBNF some extra conventions to handle them.
Section Lexer definitions explains lexer rules. Some aspects of a language belong to its lexical structure rather than its grammar, and are more naturally described by regular expressions than by BNF rules. We have therefore added to LBNF two rule formats to define the lexical structure: tokens and comments.
Section LBNF pragmas explains pragmas. Pragmas are rules instructing the BNFC grammar compiler to treat some rules of the grammar in certain special ways: to reduce the number of entrypoints or to treat some syntactic forms as internal only.
Section LBNF macros explains macros. Macros are syntactic sugar for potentially large groups of rules and help to write grammars concisely. This is both for the writer’s and the reader’s convenience; among other things, macros naturally force certain groups of rules to go together, which could otherwise be spread arbitrarily in the grammar.
Section Layout syntax explains layout syntax, which is a non-context-free feature present in some programming languages. LBNF has a set of rule formats for defining a limited form of layout syntax. It works as a preprocessor that translates layout syntax into explicit structure markers. Note: Only the Haskell backends (includes Agda) implement the layout feature.
Abstract syntax conventions¶
Predefined basic types¶
The first convention are predefined basic types. Basic types, such as integer and character, can of course be defined in LBNF, for example:
Char_a. Char ::= "a" ;
Char_b. Char ::= "b" ;
This is, however, cumbersome and inefficient. Instead, we have decided to extend our formalism with predefined basic types, and represent their grammar as a part of lexical structure. These types are the following, as defined by LBNF regular expressions (see Lexer definitions for the regular expression syntax):
Type
Integerof integers, defineddigit+Type
Doubleof floating point numbers, defineddigit+ '.' digit+ ('e' '-'? digit+)?Type
Charof characters (in single quotes), defined'\'' ((char - ["'\\"]) | ('\\' ["'\\tnrf"])) '\''Type
Stringof strings (in double quotes), defined'"' ((char - ["\"\\"]) | ('\\' ["\"\\tnrf"]))* '"'Type
Identof (Haskell) identifiers, definedletter (letter | digit | '_' | '\'')*
In the abstract syntax, these types are represented as corresponding
types of each language, except Ident, for which no such type exists. It
is treated as a newtype for String in Haskell,
newtype Ident = Ident String
as String in Java, as a typedef to char* in C and vanilla C++,
and as typedef to std::string in C++ using the
Standard Template Library (STL).
As the names of the types may suggest, the lexer produces high-precision variants for integers and floats. Authors of applications can truncate these numbers later if they want to have low precision instead.
Note
Terminals appearing in rules take precedence over Ident. E.g.,
if terminal "where" appears in any rule, the word where
will never be parsed as an Ident.
Semantic dummies¶
Sometimes the concrete syntax of a language includes rules that make no semantic difference. An example is a BNF rule making the parser accept extra semicolons after statements:
Stm ::= Stm ";" ;
As this rule is a semantic no-ops, we do not want to represent it by a constructors in the abstract syntax. Instead, we introduce the following convention:
A rule label can be an underscore _, which does not add anything to the syntax tree.
Thus, we can write the following rule in LBNF:
_ . Stm ::= Stm ";" ;
Underscores are of course only meaningful as replacements of one-argument constructors where the value type is the same as the argument type. Semantic dummies leave no trace in the pretty-printer. Thus, for instance, the pretty-printer “normalizes away” extra semicolons.
Precedence levels¶
A common idiom in (ordinary) BNF is to use indexed variants of categories to express precedence levels:
Exp2 ::= Integer ;
Exp1 ::= Exp1 "*" Exp2 ;
Exp ::= Exp "+" Exp1 ;
Exp2 ::= "(" Exp ")" ;
Exp1 ::= Exp2 ;
Exp ::= Exp1 ;
The precedence level regulates the order of parsing, including associativity. Parentheses lift an expression of any level to the highest level.
A straightforward labelling of the above rules creates a grammar that
does have the desired recognition behavior, as the abstract syntax is
cluttered with type distinctions (between Exp, Exp1, and Exp2) and
constructors (from the last three rules) with no semantic content. The
BNF Converter solution is to distinguish among category symbols those
that are just indexed variants of each other:
A category symbol can end with an integer index (i.e. a sequence of digits), and is then treated as a type synonym of the corresponding non-indexed symbol.
Thus, Exp1 and Exp2 are indexed variants of Exp.
Transitions between indexed variants are semantic no-ops, and we do not want to represent them by constructors in the abstract syntax. To achieve this, we extend the use of underscores to indexed variants. The example grammar above can now be labelled as follows:
EInt. Exp2 ::= Integer ;
ETimes. Exp1 ::= Exp1 "*" Exp2 ;
EPlus. Exp ::= Exp "+" Exp1 ;
_. Exp2 ::= "(" Exp ")" ;
_. Exp1 ::= Exp2 ;
_. Exp ::= Exp1 ;
In Haskell, for instance, the datatype of expressions becomes simply
data Exp = EInt Integer | ETimes Exp Exp | EPlus Exp Exp
and the syntax tree for 2 * ( 3 + 1 ) is
ETimes (EInt 2) (EPlus (EInt 3) (EInt 1))
Indexed categories can be used for other purposes than precedence, since the only thing we can formally check is the type skeleton (see the section The type-correctness of LBNF rules). The parser does not need to know that the indices mean precedence, but only that indexed variants have values of the same type. The pretty-printer, however, assumes that indexed categories are used for precedence, and may produce strange results if they are used in some other way.
Hint
See Section Coercions for a concise way of defining dummy coercion rules.
Polymorphic lists¶
It is easy to define monomorphic list types in LBNF:
NilDef. ListDef ::= ;
ConsDef. ListDef ::= Def ";" ListDef ;
However, compiler writers in languages like Haskell may want to use predefined polymorphic lists, because of the language support for these constructs. LBNF permits the use of Haskell’s list constructors as labels, and list brackets in category names:
[]. [Def] ::= ;
(:). [Def] ::= Def ";" [Def] ;
As the general rule, we have
[C], the category of lists of typeC,
[]and(:), the Nil and Cons rule labels,
(:[]), the rule label for one-element lists.
The third rule label is used to place an at-least-one restriction, but also to permit special treatment of one-element lists in the concrete syntax.
In the LaTeX document (for stylistic reasons) and in the Happy file (for
syntactic reasons), the category name [C] is replaced by ListC.
To prevent clashes, ListC may not be at the same time used
explicitly in the grammar.
The list notation can also be seen as a variant of the Kleene star and plus, and hence as an ingredient from Extended BNF.
Some programming languages (such as C) have no parametric polymorphism. The respective backends then generate monomorphic variants of lists.
Hint
See Section Terminators and separators for concise ways of defining lists by just giving their terminators or separators.
The type-correctness of LBNF rules¶
It is customary in parser generators to delegate the checking of certain errors to the target language. For instance, a Happy source file that Happy processes without complaints can still produce a Haskell file that is rejected by Haskell. In the same way, the BNF converter delegates some checking to the generated language (for instance, the parser conflict check). However, since it is always the easiest for the programmer to understand error messages related to the source, the BNF Converter performs some checks, which are mostly connected with the sanity of the abstract syntax.
The type checker uses a notion of the category skeleton or type of a rule, which is of the form
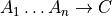
where 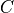 is the unindexed left-hand-side non-terminal and
is the unindexed left-hand-side non-terminal and
 is the (possibly empty)
sequence of unindexed right-hand-side
non-terminals of the rule. In other words, the category skeleton of a
rule expresses the abstract-syntax type of the semantic action
associated to that rule.
is the (possibly empty)
sequence of unindexed right-hand-side
non-terminals of the rule. In other words, the category skeleton of a
rule expresses the abstract-syntax type of the semantic action
associated to that rule.
We also need the notions of a regular category and a regular rule
label. Briefly, regular labels and categories are the user-defined
ones. More formally, a regular category is none of
[C], Integer, Double, Char, String and Ident,
or the types
defined by token rules (Section The token rule). A regular rule label is none
of _, [], (:), and (:[]).
The type checking rules are now the following:
A rule labelled by
_must have a category skeleton of form.
A rule labelled by
[]must have a category skeleton of form.
A rule labelled by
(:)must have a category skeleton of form.
A rule labelled by
(:[])must have a category skeleton of form.
Only regular categories may have productions with regular rule labels.
Every regular category occurring in the grammar must have at least one production with a regular rule label.
All rules with the same regular rule label must have the same category skeleton.
The second-last rule corresponds to the absence of empty data types in Haskell. The last rule could be strengthened so as to require that all regular rule labels be unique: this is needed to guarantee error-free pretty-printing. Violating this strengthened rule currently generates only a warning, not a type error.
Defined labels¶
LBNF gives support for syntax tree constructors that are eliminated during parsing, by following semantic definitions. Here is an example: a core statement language:
Assign. Stm ::= Ident "=" Exp ;
Block. Stm ::= "{" [Stm] "}" ;
While. Stm ::= "while" "(" Exp ")" Stm ;
If. Stm ::= "if" "(" Exp ")" Stm "else" Stm ;
We now want to have some syntactic sugar. Note that the labels for these rules all start with a lowercase letter, indicating that they correspond to defined functions rather than nodes in the abstract syntax tree.
if. Stm ::= "if" "(" Exp ")" Stm "endif" ;
for. Stm ::= "for" "(" Stm ";" Exp ";" Stm ")" Stm ;
inc. Stm ::= Ident "++" ;
Functions are defined using the define keyword. Definitions have the
form:
define f x1 .. xn = e
where e is an expression in applicative form using rule labels,
other defined functions, lists and literals.
define if e s = If e s (Block []) ;
define for i c s b = Block [i, While c (Block [b, s])] ;
define inc x = Assign x (EOp (EVar x) Plus (EInt 1)) ;
terminator Stm ";" ;
Another use of defined functions is to simplify the abstract syntax for binary operators. Instead of one node for each operator we want to have a general node (EOp) for all binary operator applications.
_. Op ::= Op1 ;
_. Op ::= Op2 ;
Less. Op1 ::= "<" ;
Equal. Op1 ::= "==" ;
Plus. Op2 ::= "+" ;
Minus. Op2 ::= "-" ;
op. Exp ::= Exp1 Op1 Exp1 ;
op. Exp1 ::= Exp1 Op2 Exp2 ;
EInt. Exp2 ::= Integer ;
EVar. Exp2 ::= Ident ;
coercions Exp 2;
Care has to be taken to make sure that the pretty printer outputs enough parentheses.
internal EOp. Exp ::= Exp1 Op Exp1 ;
define op e1 o e2 = EOp e1 o e2 ;
Note
Implementing syntactic sugar via define maybe be good for rapid
prototyping, but has some drawbacks for more serious programming
language implementation: Since the parser already expands the
syntactic sugar, subsequent parts of the front end, like scope or
type checkers, do not report errors in sugar in terms of what the
user may have written, but what arrives at the checker. For
instance, xs++ for an array variable xs will not report a
problem in xs++, but rather in its expansion x = x + 1.
Lexer definitions¶
The token rule¶
The token rule enables the LBNF programmer to define new lexical types using a simple regular expression notation. For instance, the following rule defines the type of identifiers beginning with upper-case letters.
token UIdent (upper (letter | digit | '_')*) ;
The type UIdent becomes usable as an LBNF nonterminal and as a type in
the abstract syntax. Each token type is implemented by a newtype in
Haskell, as a String in Java, and as a typedef to char* in C etc.
The regular expression syntax of LBNF is specified in the Appendix. The abbreviations with strings in brackets need a word of explanation:
["abc7%"]denotes the union of the characters ‘a‘b’ ‘c’ ‘7’ ‘%’
{"abc7%"}denotes the sequence of the characters ‘a’ ‘b’ ‘c’ ‘7’ ‘%’
The atomic expressions upper, lower, letter, and digit denote the
isolatin1 character classes corresponding to their names.
The expression char matches any unicode character, and the
“epsilon” expression eps matches the empty string. Thus eps is
equivalent to {""}, whereas the empty language is expressed by [""].
Note
Terminals appearing in rules take precedence over any token.
E.g., if terminal "Fun" appears in any rule, the word Fun
will never be parsed as a UIdent.
Note
As of October 2020, the empty language is only handled by the Java backend.
The position token rule¶
Any token rule can be
modified by the word position, which has the effect that the datatype defined
will carry position information. For instance,
position token PIdent (letter (letter|digit|'_'|'\'')*) ;
creates in Haskell the datatype definition
newtype PIdent = PIdent ((Int,Int),String)
where the pair of integers indicates the line and column of the first character of the token. The pretty-printer omits the position component.
(As of October 2020, the cpp-nostl backend (C++ without using the STL)
does not implement position tokens.)
The comment rule¶
Comments are segments of source code that include free text and are
not passed to the parser. The natural place to deal with them is in the
lexer. The comment rule instructs the lexer generator to treat certain
pieces of text as comments.
The comment rule takes one (for line comments) or two string arguments (for block comments). The first string defines how a comment begins. The second, optional string marks the end of a comment; if it is not given then the comment is ended by a newline. For instance, the Java comment convention is defined as follows:
comment "//" ;
comment "/*" "*/" ;
Note: The generated lexer does not recognize nested block comments, nor does it respect quotation, as in strings. In the following snippet
/* Commenting out...
printf("*/");
*/
the lexer will consider the block comment to be closed before ");.
LBNF pragmas¶
Internal pragmas¶
Sometimes we want to include in the abstract syntax structures that are not part of the concrete syntax, and hence not parsable. They can be, for instance, syntax trees that are produced by a type-annotating type checker. Even though they are not parsable, we may want to pretty-print them, for instance, in the type checker’s error messages. To define such an internal constructor, we use a pragma
"internal" Rule ";"
where Rule is a normal LBNF rule. For instance,
internal EVarT. Exp ::= "(" Identifier ":" Type ")";
introduces a type-annotated variant of a variable expression.
Entry point pragmas¶
The BNF Converter generates, by default, a parser for every category in the grammar. This is unnecessarily rich in most cases, and makes the parser larger than needed. If the size of the parser becomes critical, the entry points pragma enables the user to define which of the parsers are actually exported.
For instance, the following pragma defines Stm, Exp2 and lists
of identifiers [Ident] to be the only entry points:
entrypoints Stm, Exp2, [Ident];
LBNF macros¶
Terminators and separators¶
The terminator macro defines a pair of list rules by what token
terminates each element in the list. For instance,
terminator Stm ";" ;
tells that each statement (Stm) is terminated with a semicolon
(;). It is a shorthand for the pair of rules
[]. [Stm] ::= ;
(:). [Stm] ::= Stm ";" [Stm] ;
The qualifier nonempty in the macro makes one-element list to be the
base case. Thus
terminator nonempty Stm ";" ;
is shorthand for
(:[]). [Stm] ::= Stm ";" ;
(:). [Stm] ::= Stm ";" [Stm] ;
The terminator can be specified as empty "". No token is introduced
then, but e.g.
terminator Stm "" ;
is translated to
[]. [Stm] ::= ;
(:). [Stm] ::= Stm [Stm] ;
The separator macro is similar to terminator, except that the
separating token is not attached to the last element. Thus
separator Stm ";" ;
means
[]. [Stm] ::= ;
(:[]). [Stm] ::= Stm ;
(:). [Stm] ::= Stm ";" [Stm] ;
whereas
separator nonempty Stm ";" ;
means
(:[]). [Stm] ::= Stm ;
(:). [Stm] ::= Stm ";" [Stm] ;
Notice that, if the empty token "" is used, there is no difference
between terminator and separator.
Problem. The grammar generated from a separator without
nonempty will actually also accept a list terminating with a
semicolon, whereas the pretty-printer “normalizes” it away. This might
be considered a bug, but a set of rules forbidding the terminating
semicolon would be more complicated:
[]. [Stm] ::= ;
_. [Stm] ::= [Stm]1 ;
(:[]). [Stm]1 ::= Stm ;
(:). [Stm]1 ::= Stm ";" [Stm]1 ;
This is unfortunately not legal LBNF, since precedence levels for lists are not supported.
Coercions¶
The coercions macro is a shorthand for a group of rules translating
between precedence levels. For instance,
coercions Exp 3 ;
is shorthand for
_. Exp ::= Exp1 ;
_. Exp1 ::= Exp2 ;
_. Exp2 ::= Exp3 ;
_. Exp3 ::= "(" Exp ")" ;
Because of the total coverage of these coercions, it does not matter whether
the integer indicating the highest level (here 3) is bigger than the
highest level actually occurring, or whether there are some other levels
without productions in the grammar.
However, unused levels may bloat the generated parser definition file
(e.g., the Happy file in case of Haskell) unless the backend implements
some sort of dead-code removal. (As of October 2020, no backend
implements such clever analysis.)
Hint
Coerced categories (e.g. Exp2) can also be used in other rules. For
instance, given the following grammar:
EInt. Exp2 ::= Integer;
EAdd. Exp1 ::= Exp1 "+" Exp2;
you might want to use Exp2 instead of simply Exp to force the usage
of parenthesis around non-trivial expressions. For instance, Foo. F ::=
"foo" Exp2 ; will accept foo 42 or foo (1 + 1) but not
foo 1 + 1.
You can even use coerced categories in lists and give them different separators/terminators:
separator Exp "," ;
separator Exp2 ";" ;
Rules¶
The rules macro is a shorthand for a set of rules from which labels
are generated automatically. For instance,
rules Type ::= Type "[" Integer "]" | "float" | "double" | Type "*" | Ident ;
is shorthand for
Type1. Type ::= Type "[" Integer "]" ;
Type_float. Type ::= "float" ;
Type_double. Type ::= "double" ;
Type2. Type ::= Type "*" ;
TypeIdent. Type ::= Ident ;
The labels are created automatically. A label starts with the value category name. If the production has just one item, which is moreover possible as a part of an identifier, that item is used as a suffix. In other cases, an integer suffix is used. No global checks are performed when generating these labels. Label name clashes leading to type errors are captured by BNFC type checking on the generated rules.
Layout syntax¶
Layout syntax is a means of using indentation to group program elements. It is used in some languages, e.g. Agda, Haskell, and Python. Layout syntax is a rather experimental feature of BNFC and only supported by the Haskell-family backends, so the reader might want to skip this section on the first reading.
The pragmas layout, layout stop, and layout toplevel define a layout
syntax for a language.
From these pragmas, a Haskell module named Layout, the layout
resolver, is created to be plugged in between lexer and parser. This
module inserts extra tokens (braces and semicolons) into the token
stream coming from the lexer, according to the rules explained below.
Hint
To get layout resolution in other backends, the generated Haskell layout resolver could to be hand-ported to the desired programming language. Alternatively, the generated Haskell lexer and layout resolver could be turned into a stand-alone preprocessor that lexes a file into tokens, inserts the extra tokens according to the layout rules, and prints the tokens back into a character stream that can be further processed by the lexer and parser written in the desired programming language.
The layout pragmas of BNFC are not powerful enough to handle the full layout rule of Haskell 98, but they suffice for the “regular” cases.
For a feature overview, a first simple example: a grammar for trees.
A Tree be a number (the payload) followed by br plus a
(possibly empty) list of subtrees:
Node. Tree ::= Integer "br" "{" [Tree] "}" ;
separator Tree ";" ;
layout "br" ;
The lists are enclosed in braces and separated by semicolons. This is the only syntax supported by the layout mechanism for the moment.
The generated parser can process this example:
0 br
1 br
2 br
3 br
4 br
5 br
6 br
7 br
Thanks to the layout resolution, this is treated in the same way as the following input would be treated without layout support:
0 br
{ 1 br
{ 2 br {}
; 3 br {}
}
; 4 br
{ 5 br
{ 6 br {}
}
}
; 7 br {}
}
The layout resolver produces, more precisely, the following equivalent intermediate text (in form of a token stream):
0 br{
1 br{
2 br{
}; 3 br{
}
}; 4 br{
5 br{
6 br{
}
}
}; 7 br{
}}
Now to a more realistic example, found in the the grammar of the logical framework Alfa. (Caveat: This example is a bit dated…)
layout "of", "let", "where", "sig", "struct" ;
The first line says that "of", "let", "where", "sig",
"struct" are layout words, i.e. start a layout list. A layout list is a
list of expressions normally enclosed in curly brackets and separated by
semicolons, as shown by the Alfa example:
ECase. Exp ::= "case" Exp "of" "{" [Branch] "}" ;
separator Branch ";" ;
When the layout resolver finds the token of in the code (i.e. in the
sequence of its lexical tokens), it checks if the next token is an
opening curly bracket. If it is, nothing special is done until a layout
word is encountered again. The parser will expect the semicolons and the
closing bracket to appear as usual.
But, if the token 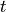 following
following of is not an opening curly
bracket, a bracket is inserted, and the start column of 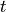 (or the column after the current layout column, whichever is bigger)
is remembered as the position at which the elements of the layout list must
begin. Semicolons are inserted at those positions. When a token is
eventually encountered left of the position of
(or the column after the current layout column, whichever is bigger)
is remembered as the position at which the elements of the layout list must
begin. Semicolons are inserted at those positions. When a token is
eventually encountered left of the position of 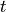 (or an
end-of-file), a closing bracket is inserted at that point.
(or an
end-of-file), a closing bracket is inserted at that point.
Nested layout blocks are allowed, which means that the layout resolver maintains a stack of positions. Pushing a position on the stack corresponds to inserting a left bracket, and popping from the stack corresponds to inserting a right bracket.
Here is an example of an Alfa source file using layout:
c :: Nat = case x of
True -> b
False -> case y of
False -> b
Neither -> d
d = case x of True -> case y of False -> g
x -> b
y -> h
Here is what it looks like after layout resolution:
c :: Nat = case x of {
True -> b
;False -> case y of {
False -> b
};Neither -> d
};d = case x of {True -> case y of {False -> g
;x -> b
};y -> h} ;
There are two more layout-related pragmas. The layout stop pragma, as in
layout stop "in" ;
tells the resolver that the layout list can be exited with some stop
words, like in, which exits a let list. It is no error in the resolver
to exit some other kind of layout list with in, but an error will show
up in the parser.
The layout toplevel pragma tells that the whole source file is a layout
list, even though no layout word indicates this. The position is the
first column, and the resolver adds a semicolon after every paragraph
whose first token is at this position. No curly brackets are added. The
Alfa file above is an example of this, with two such semicolons added.
Stacking layout keywords¶
Since version 2.9.2, the layout processor supports stacking of layout keywords on the same line. Consider the following fragment of an Agda-ish grammar:
Module. Decl ::= "module" Ident "where" "{" [Decl] "}" ;
Private. Decl ::= "private" "{" [Decl] "}" ;
TypeSig. Decl ::= Ident ":" Ident ;
separator Decl ";" ;
layout "where", "private" ;
This grammar allows us to define simple Agda modules that contain a
list of declarations, each of which can be a module, a private block
or a type signature. Lists of declarations are enclosed in braces
and separated by semicolons, and introduced by the layout keywords
where and private.
We may want to define a private module, and instead of two subsequent indentations:
private
module M where
A : Set
we wish to stack the two layout introductions on a single line:
private module M where
A : Set
This is not supported by the layout logic up to BNFC 2.9.1, as we
would fix the layout column for the private block to column 8, the
column of token module. The token A following the next layout
keyword where lives at column 2 which is below 8, thus, the
private block would be closed here. But with private
closing, the inner block module M where also needs to close, and
then the declaration A : Set is simply misindented. Thus, this
gives a parse error with BNFC 2.9.1.
The layout processor produced by BNFC 2.9.2 instead marks the layout
column 8 of the private block as tentative since the token
module following the layout keyword private is on the same
line. On the contrary, the layout column 2 of the module block is
definitive since the token A following the layout keyword
where is at a later line. When checking whether a new layout
column is valid, tentative layout columns get ignored, thus it is only
checked that 2 > 0, not that 2 > 8. When at some
point the module block will be closed because we encounter a token
indented less than 2, the private block will be closed as well
since its indentation column 8 is also greated than the indentation of
the encountered token.
In general, when encountering a new line, we switch the top layout columns to definitive if they are still tentative. For instance, consider the following situation:
private module M where A : Set
module N where
Bad : Set
At the end of the first line, we have two tentative layout columns, 8
(column of module) and 23 (column of A). Since now we have no
pending layout keyword left in this line, we switch the layout columns
to definitive when we see the next token module on a new line.
The first module closes here, leaving us with definitive layout
column 8. This prevents that we assign to the subsequent block
module N with layout keyword where the column 2 (token
Bad). Instead, this block gets a default column, 8+1. When
processing token Bad both blocks get closed since 2 < 8 and 2 < 8+1.
But then Bad is
misindented, yielding the expected parse error.
The changes introduced for stacking layout keywords are backwards compatible in the following sense: A layout-aware parser generated by BNFC 2.9.2 accepts all texts that were soundly accepted by the respective parser generated by BNFC 2.9.1 and before. Further, the same syntax trees are generated for these accepted texts.
An optimization: left-recursive lists¶
The BNF representation of lists is right-recursive, following the list
constructor in Haskell and most other languages. Right-recursive lists,
however, require linear stack space in a shift-reduce parser (such as
the LR parser family). This can be a problem when the size of the
stack is limited (e.g. in bison generated parsers).
A right-recursive list definition
[]. [Stm] ::= ;
(:). [Stm] ::= Stm ";" [Stm] ;
becomes left recursive under the left-recursion transformation:
[]. [Stm] ::= ;
(flip (:)). [Stm] ::= [Stm] Stm ";" ;
However, the thus parsed lists need to be reversed when used as part of another rule.
For backends that target stack-restricted parsers (C, C++, Java), the BNF Converter automatically performs the left-recursion transformation for pairs of rules of the form
[]. [C] ::= ;
(:). [C] ::= C x [C] ;
where C is any category and x is any sequence of terminals (possibly empty). These rules can, of course, be generated from the terminator macro (Section Terminators and separators).
Notice. The transformation is currently not performed if the
one-element list is the base case.
It is also not performed in the Haskell backend that generates parsers with a
heap-allocated stack via happy.
Appendix: LBNF Specification¶
This document was originally automatically generated by the BNF-Converter. It was generated together with the lexer, the parser, and the abstract syntax module, to guarantee that the document matches the implementation of the language. In the present form, the document has gone through some manual editing.
The lexical structure of BNF¶
Identifiers¶
Identifiers are unquoted strings beginning with a letter, followed by any combination of letters, digits, and the character _, reserved words excluded.
Literals¶
String literals String have the form " 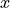
", where 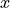 is any
sequence of any characters except
is any
sequence of any characters except " unless preceded by \.
Integer literals Integer are nonempty sequences of digits.
Character literals Char have the form ' 
' , where  is any
single character.
is any
single character.
Reserved words and symbols¶
The set of reserved words is the set of terminals appearing in the grammar. Those reserved words that consist of non-letter characters are called symbols, and they are treated in a different way from those that are similar to identifiers. The lexer follows rules familiar from languages like Haskell, C, and Java, including longest match and spacing conventions.
The reserved words used in BNF are the following:
char coercions comment
digit
entrypoints eps
internal
layout letter lower
nonempty
position
rules
separator stop
terminator token toplevel
upper
The symbols used in BNF are the following:
; . ::=
[ ] _
( : )
, | -
* + ?
{ }
The syntactic structure of LBNF¶
Non-terminals are enclosed between < and >.
The symbols ::= (production), | (union) and ε (empty rule)
belong to the BNF notation.
All other symbols are terminals
(as well as sometimes even ::= and |).
<Grammar> ::= <ListDef>
<ListDef>
::= ε
| <Def>
| <Def> ; <ListDef>
| ; <ListDef>
<Def>
::= entrypoints <ListCat>
| <Label> . <Cat> ::= <ListItem>
| internal <Label> . <Cat> ::= <ListItem>
| separator <MinimumSize> <Cat> <String>
| terminator <MinimumSize> <Cat> <String>
| coercions <Identifier> <Integer>
| rules <Identifier> ::= <ListRHS>
| comment <String>
| comment <String> <String>
| token <Identifier> <Reg>
| position token <Identifier> <Reg>
| layout <ListString>
| layout stop <ListString>
| layout toplevel
<ListCat>
::= <Cat>
| <Cat> , <ListCat>
<ListItem>
::= ε
| <Item> <ListItem>
<Item>
::= <String>
| <Cat>
<Cat>
::= [ <Cat> ]
| <Identifier>
<Label>
::= <Identifier>
| _
| [ ]
| ( : )
| ( : [ ] )
<ListString>
::= <String>
| <String> , <ListString>
<ListRHS>
::= <RHS>
| <RHS> | <ListRHS>
<RHS> ::= <ListItem>
<MinimumSize>
::= ε
| nonempty
<Reg>
::= <Reg> | <Reg1>
| <Reg1>
<Reg1>
::= <Reg1> − <Reg2>
| <Reg2>
<Reg2>
::= <Reg2> <Reg3>
| <Reg3>
<Reg3>
::= <Reg3> *
| <Reg3> +
| <Reg3> ?
| eps
| <Char>
| [ <String> ]
| { <String> }
| digit
| letter
| upper
| lower
| char
| ( <Reg> )
Comments¶
--.{-and-}.